Edukiper.com - Operasi Himpunan. Himpunan adalah kumpulan benda atau obyek atau hal yang didefenisikan secara jelas. Sebuah himpunan memiliki anggota himpunan atau elemen. Elemen himpunan adalah benda atau objek yang dimuat di dalam suatu himpunan itu sendiri. Anggota himpunan umumnya ditulis di antara kurung kurawal. Lalu, bisakah kita melakukan operasi antar himpunan? Bagaimana rumus dan sifat operasi antar himpunan?
Sebelum membahas bagaimana operasi antar himpunan dapat dilakukan, ada baiknya kita kembali mengingat bagaimana cara penulisan himpunan. Penulisan himpunan dapat dilakukan dengan cara pendaftaran atau dengan cara deskripsi menggunakan kata-kata.
Cara pendaftaran dilakukan dengan mendaftarkan semua anggota himpunan di antara dua kurung kurawal, sebagai contoh perhatikan penulisan dua himpunan secara mendaftar berikut ini:
1). A = {0, 1, 4, 8}
2). B = {p, q, r, s}
Cara deskripsi atau menggunakan kata-kata dilakukan dengan mencantumkan syarat keanggotaan di antara dua kurung kurawal, perhatikan contoh :
1). A = {x | x bilangan asli}
2). B = {faktor dari 12}.
#1 Irisan Himpunan
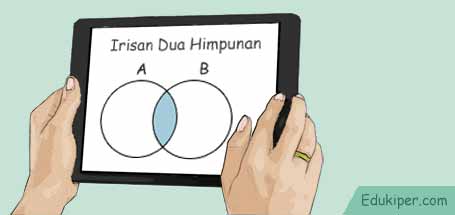
Irisan dari dua himpunan A dan B adalah satu himpunan yang anggotanya adalah anggota himpunan A yang juga merupakan anggota dari himpunan B. Dengan kata lain, anggota himpunan dari irisan A dan B adalah anggota himpunan A yang juga ada di himpunan B.
Irisan umumnya disimbolkan dengan "∩". Dengan demikian, irisan A dan B dapat ditulis A ∩ B, dan berlaku persamaan berikut : A ∩ B = {x | x E A dan x E B}.
Contoh :
Diberikan dua himpunan A dan B, tentukan irisannya :
A = {2, 4, 5, 8}
B = {1, 2, 3, 4}
Penyelesaian :
A ∩ B = {2, 4}.
#2 Gabungan Himpunan
Gabungan antara himpunan A dan himpunan B adalah suatu himpunan yang anggotanya berasal dari himpunan A atau B atau keduanya. Gabungan biasanya ditulis dengan A ∪ B, dan berlaku hubungan A ∪ B = {x | x E A atau x E B}.
Contoh :
Diberikan dua himpunan A dan B, tentukan gabungannya :
A = {1, 3, 7}
B = {2, 3, 4, 5}
Penyelesaian :
A ∪ B = {1, 2, 3, 4, 5, 7}.
⇒ Irisan : A ∩ B = B ∩ A
⇒ Gabungan : A ∪ B = B ∪ A
#2 Sifat Asosiatif
⇒ Irisan : A ∩ (B ∩ C) = (A ∩ B) ∩ C
⇒ Gabungan : A ∪ (B ∪ C) = (A ∪ B) ∪ C
#3 Sifat Distributif
Irisan terhadap gabungan :
⇒ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Gabungan terhadap irisan :
⇒ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
#4 Dalil de Morgan
⇒ Irisan : (A ∩ B)' = A' ∪ B'
⇒ Gabungan : (A ∪ B)' = A' ∩ B'
Dua buah himpunan A dan B disebut saling berpotongan (tidak lepas) jika ada anggota himpunan A yang juga menjadi anggota himpunan B. Untuk dua himpunan yang berpotongan, berlaku:
#2 Dua Himpunan Saling Lepas
Dua buah himpunan A dan B disebut saling lepas jika tidak ada anggota himpunan A yang menjadi anggota himpunan B atau sebaliknya. Untuk dua himpunan saling lepas, berlaku:
Demikianlah pembahasan singkat mengenai operasi antar himpunan, sifat-sifat operasi himpunan, dan rumus operasi himpunan atau kardinalitas. Jika artikel ini bermanfaat, silahkan bagikan melalui tombol share yang tersedia.
Sebelum membahas bagaimana operasi antar himpunan dapat dilakukan, ada baiknya kita kembali mengingat bagaimana cara penulisan himpunan. Penulisan himpunan dapat dilakukan dengan cara pendaftaran atau dengan cara deskripsi menggunakan kata-kata.
Cara pendaftaran dilakukan dengan mendaftarkan semua anggota himpunan di antara dua kurung kurawal, sebagai contoh perhatikan penulisan dua himpunan secara mendaftar berikut ini:
1). A = {0, 1, 4, 8}
2). B = {p, q, r, s}
Cara deskripsi atau menggunakan kata-kata dilakukan dengan mencantumkan syarat keanggotaan di antara dua kurung kurawal, perhatikan contoh :
1). A = {x | x bilangan asli}
2). B = {faktor dari 12}.
A. Operasi Antarhimpunan
#1 Irisan Himpunan
Irisan dari dua himpunan A dan B adalah satu himpunan yang anggotanya adalah anggota himpunan A yang juga merupakan anggota dari himpunan B. Dengan kata lain, anggota himpunan dari irisan A dan B adalah anggota himpunan A yang juga ada di himpunan B.
Irisan umumnya disimbolkan dengan "∩". Dengan demikian, irisan A dan B dapat ditulis A ∩ B, dan berlaku persamaan berikut : A ∩ B = {x | x E A dan x E B}.
Contoh :
Diberikan dua himpunan A dan B, tentukan irisannya :
A = {2, 4, 5, 8}
B = {1, 2, 3, 4}
Penyelesaian :
A ∩ B = {2, 4}.
#2 Gabungan Himpunan
Gabungan antara himpunan A dan himpunan B adalah suatu himpunan yang anggotanya berasal dari himpunan A atau B atau keduanya. Gabungan biasanya ditulis dengan A ∪ B, dan berlaku hubungan A ∪ B = {x | x E A atau x E B}.
Contoh :
Diberikan dua himpunan A dan B, tentukan gabungannya :
A = {1, 3, 7}
B = {2, 3, 4, 5}
Penyelesaian :
A ∪ B = {1, 2, 3, 4, 5, 7}.
B. Sifat Operasi Himpunan
#1 Sifat Komutatif⇒ Irisan : A ∩ B = B ∩ A
⇒ Gabungan : A ∪ B = B ∪ A
#2 Sifat Asosiatif
⇒ Irisan : A ∩ (B ∩ C) = (A ∩ B) ∩ C
⇒ Gabungan : A ∪ (B ∪ C) = (A ∪ B) ∪ C
#3 Sifat Distributif
Irisan terhadap gabungan :
⇒ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Gabungan terhadap irisan :
⇒ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
#4 Dalil de Morgan
⇒ Irisan : (A ∩ B)' = A' ∪ B'
⇒ Gabungan : (A ∪ B)' = A' ∩ B'
C. Rumus Operasi (Kardinalitas)
#1 Dua Himpunan BerpotonganDua buah himpunan A dan B disebut saling berpotongan (tidak lepas) jika ada anggota himpunan A yang juga menjadi anggota himpunan B. Untuk dua himpunan yang berpotongan, berlaku:
| n(A ∪ B) = n(S) − n(A ∪ B)' |
| n(A ∪ B) = n(A) + n(B) − n(A ∩ B) |
#2 Dua Himpunan Saling Lepas
Dua buah himpunan A dan B disebut saling lepas jika tidak ada anggota himpunan A yang menjadi anggota himpunan B atau sebaliknya. Untuk dua himpunan saling lepas, berlaku:
| n(A ∪ B) = n(A) + n(B) |
Demikianlah pembahasan singkat mengenai operasi antar himpunan, sifat-sifat operasi himpunan, dan rumus operasi himpunan atau kardinalitas. Jika artikel ini bermanfaat, silahkan bagikan melalui tombol share yang tersedia.
0 comments :
Post a Comment